Basic trading strategies using European options (part 1 of 2)

November 10, 2018

Basic trading strategies using European options (part 1 of 2)

Properties of the hedging of strategies with options;
Optimization of strategy entries;
Single option strategies;
Bull / Bear spreads;
Butterfly spreads;
Straddle and Strangles (part 2 of 2);
Calendar spreads (part 2 of 2);

Hey, all! What´s up?

Derivatives can be informally defined as a product which produces a payoff that depends on the value (or behaviour) of determined underlying asset (or basket of assets). Trading a derivative means that the holder and the seller either expect some behavior of the underlying asset or are trying to hedge some position in the underlying asset. Here, I´ll discuss strategies for both cases, speculation and hedge.

Several types of options are traded in the market, the simplest types are plain vanilla European calls and puts. Calls give to the holder the right (but not the obligation) to buy an asset by determined strike price at determined date denoted as maturity. A put is similar to a call, but gives the holder the right to sell an asset by determined strike price.

The results and examples presented hereafter are calculated using the Black-Scholes model, whose implementation provided in this post as well as the formulas for the calculation. Different derivations of the Black-Scholes equation are provided in this post, and an in-depth analysis of one its main assumptions is given here. Since we are using Black-Scholes model, smiles and skews are not considered.

Single option strategies:

The simplest strategies involving plain vanilla European options are buying a put (call) when one wants to hedge a long (short) position in an asset whose value might decreases (increases) until the maturity of the option.

The price of the a single call and a single put for different times to maturity $T-t$ are given in the plots below. At $T-t=0$ the price is the payoff of the option. It is worth remembering that since the graphs are obtained by the Black-Scholes equation, the volatility is assumed constant!

Call option

Put option

The hedging of this strategies are simply the greeks of the each option. The plots below present the values for the strategy using puts:

Other more complicated strategies can also be used depending on the expectation about the market. Further comments on the most basic ones are provided in the following:

Bull / Bear spreads:

The entire code is given here.
A bull is created when one expects an up movement of the market. It can be created by taking a long call with strike $K_1$ and shorting another call with strike $K_2$, where $K_1<K_2$. A bear is used in the opposite case of the bull, that is, when one believes the market value of the asset will decrease. It is created, for instance, by longing a put with strike $K_2$ and shorting another put with strike $K_1$, where again $K_1<K_2$. It is worth noticing that both strategies are cheaper than use a single option (like a longing a call for example) but limits the profit.

In principle, the creation of the strategy is created out-of the-money (OTM), maximizing the profit in case of the expect movement realizes itself at the maturity.

Bear spread values at different times to maturity

Bull spread valuse at different times to maturity

Another very important feature of Bulls and Bears concerns the risk compared to single option strategies. With respect to hedging of positions, single option strategies are much riskier when considering changes in the spot price, interest rate, and volatility. Although comparatively they are less susceptible to changes in time. As a conclusion, a lower number of hedging transactions are required when trading with bulls and bears than with single options. The safer nature of bulls and bears with respect to hedging is demonstrated by the greeks of these strategies. In the following, the greeks of the bear spread are presented:

Butterfly spreads:

The entire code is given here.
While bulls and bears are used when one expects a movement of the market toward a determined direction (either up or down), butterflies are used when one do not expect large movements from a determined spot price. Butterflies can be created longing a call with strike price $K_1$, shorting 2 calls with strike $K_2$, and longing one more call $K_3$, where $K_1<K_2<K_3$.

Notice that butterflies comprised of calls and puts present the exact same value, considering the same maturity and strike prices.

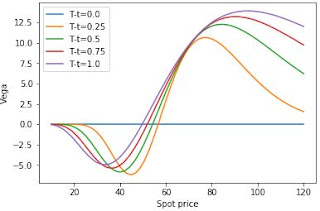
In principle, this strategy is assembled assuming $K_2$ close to the current spot price, which means that one expects a period of low volatility of the underlying asset until the maturity of the butterfly. In fact, the higher vega is around $K_2$. Comparatively, similar to bulls and bears, butterfly spread also requires less hedging comparing to single option strategies. In fact, the greeks of a butterfly strategy present lower magnitudes, mainly $\Delta$ and $\Gamma$.