Basic trading strategies using European options (part 2 of 2)

• Hedging of strategies with options;
• Optimization of strategy entries;
• Single option strategies (part 1 of 2);
• Bull / Bear spreads (part 1 of 2);
• Butterfly spreads (part 1 of 2);
• Straddle and Strangles;
• Calendar spreads;

Hey all!

In the first part of this post, we have discussed single option strategies, bull and bear strategies and butterflies. In this post, I´ll present Straddle, strangles, and calendar spreads. Before going further, it is important to mentioning that all results presented here were obtained using the assumptions of the Black-Scholes, such as presented in a previous post. Therefore, no smile, skew or term-structure is considered for the volatility.

Straddles and strangles

The entire code is given here.
Strangle are created assuming long positions in a put with strike price $K_1$ and in a call with strike price $K_2$, where $K_1<K_2$ and both with same maturity. Straddles are simply a strangle in which $K_1=K_2$. Unlike, butterflies in which one expects a period of low change in the spot price, for straddles and strangles the investor bets on a large movement of the market for any direction (up or down, simultaneously). The value of this strategy at different times to maturity is exemplified below:

The optimal entry into this strategy is obviously when both options are out-of-the-money (OTM), that is, when spot price is between $K_1$ and $K_2$. Using this optimal entry, the profit and loss plot (P&L) for the strangles, considering entries at different times to maturity, presents the following general behavior:

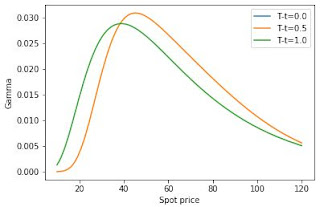
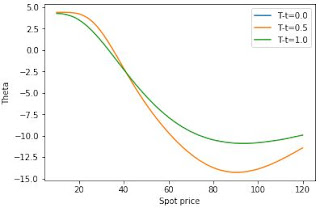
The potential gain of this strategy is in principle unlimited. However, the magnitude of the greeks is comparable or even higher than the one obtained with a single option position, as showed in the following plots:

Calendar spread:

The entire code is given here.
Until far, we have only discussed strategies in which all options present the same time to maturity. In the calendar spread, one assumes a short and a long position in two calls with the same strike, but the short position is assumed with shorter time to maturity. The payoff of this strategy is usually counted at the maturity $T-t=0$ of the short position as shown in the following plot:

Similarly to the butterfly strategy, using this strategy one does not expect large movements of the underlying asset far from the strike price $K$. The payoff at maturity of the calendar spread is broader than the one of the butterfly strategy, although calendars might be considerably more expensive than butterflies. In order to choose between butterflies or calendar spreads, one must consider trade-off mentioned before including the expected future volatility as well as the time to maturity to collect the potential payoff. Other crucial difference between both strategies is that the greeks of the calendar spread are comparatively higher than those of the butterfly, which might imply more transactions to hedge calendar spreads. The greeks are presented in the following:

I hope you have enjoyed the post. Get in contact with your suggestions and comments.

May the Force be with you.

#=================================

Diogo de Moura Pedroso

LinkedIn: www.linkedin.com/in/diogomourapedroso