Model calibration using optimization engines: an example using implied volatility

• Use of metaheuristics, particularly differential evolution in model parametrization
• calibration of implied volatility using SVI curves
• use of the scipy optimization package in Python

Hello, all!

...hitting the target...

Models can be informally defined as a set of assumptions and approximations intending to describe determined phenomena given some input values. In general, the mathematical formulation of a model depends on a certain parametrization which changes according to the considered condition. If you have a kinematic model for cannon balls, for instance, an obvious parametrization is the initial velocity of the object, which completely changes the position of the ball as a function of time. The procedure for parametrization varies for each model, in this post I´ll focus on models whose calibration is done by optimization algorithms. I´ll use as an example the calibration of the SVI curve for implied volatility obtained with the Black-Scholes model. First, I provide an overview of optimization algorithms. In the following, I present a description of the problem. Then, the objective function followed by the results. 

Models can be informally defined as a set of assumptions and approximations intending to describe determined phenomena given some input values.

Optimization overview

Optimization engines are algorithms created to compute extreme points of different models, that is, calculate minimum and/or maximum points. Analytically, the critical point of any function $f(x_1, x_2, x_3, ...)$ (expressing the model) are those at which all partial derivatives are null or put in other words the gradient is zero: $\nabla f(x_i)=0$. A simple concept for optimization engines is to iteratively calculate gradients searching for the direction of minimization of the gradient and then obtain the critical point when this gradient is below a certain specified error. These kind of deterministic methods are known as gradient methods. An obvious drawback of this kind of algorithms is the impossibility of application for non-derivable formulas, which might not be known in a first hand. In Python, one can access several gradient methods by means of the optimization package within scipy: scipy.optimize.minimize (documentation). In the following, I present a simple example:

Problems with several minimum points are known as multimodal problems. In the example above, the polynomial has two minimum points. One can notice that using the function minimize exemplified above the value of the initial guess x0 plays an essential role in the minimum point. Gradient-based methods are deterministic, therefore its final value depends uniquely on the admitted error.
Another important group of optimization algorithms are the metaheuristics. These algorithms are based on stochastic selection of populations of trial solutions, which evolve towards the solution guided by some specific strategy, such as nature-inspired ones (simulated annealing, genetic algorithm, ant colony, sea turtle life-cycle, among others). Metaheuristics does not require an initial guess and they search for the global minimum (or maximum), although the process is not guaranteed. Unlike gradient-based methods, different runs of calculation using a metaheuristic provides a different outcome due to the stochastic nature of the algorithm.
In this post, I´ll use Differential Evolution to perform model calibration. Similarly to the well-known Genetic Algorithm (GA), this metaheuristic is based on the evolution of candidate solutions towards those with lower objective function. A black-box implementation of this algorithm is available in: scipy.optimize.differential_evolution (documentation). In this algorithm, the candidate solutions of the next iterations are transformed based on the values of the current candidates according to some strategies. The input of these strategies are obtained from the candidates of the previous iteration. Several strategies are implemented in the scipy package and until version 0.15.1 is not possible to implement a customized strategy.
The two main parameters of this implementation are the recombination and the mutation. The recombination parameter indicates how likely the input of the modification strategy for the next iteration will use a mutated population or simply the current population as it is. The mutation parameter indicates the degree of change of the current population to be used as an input for the transformation strategy.

The problem: implied volatility

One of the key problems in quantitative finance is the determination of the implied volatility (IV) from the market prices of derivative contracts. Volatility of a financial asset indicates the degree of variation of the prices. In the case of a derivative whose price depends directly of the behavior of an underlying asset, the implied volatility is the one allegedly assumed by the market players when pricing the derivative. It corresponds to an expectation of the players for the volatility of the underlying asset during the future period until the maturity of the contract. The determination of the implied volatility has several applications, such as pricing exotic derivatives (non-conventional contracts), identification of arbitrage opportunities and creation of trading strategies. 

Several models can be used to fit the implied volatility form the market data. Usually, a good model for IV corresponds to the one that is able to fit well not so liquid instruments, mainly in the regions out- and in-the -money. For completeness, an out-of-the-money (OTM) region is the one in which the payoff would be zero if price of the underlying asset remains the same until the maturity. Conversely, the in-the-money (ITM) region is the one whose payoff of the contract would be non-null if the underlying asset remains constant until maturity. 

The model I´ll use in this post is the SVI (Stochastic Volatility Inspired) which will be applied for vanilla European options modeled using Black-Scholes (this post brings useful information). The most common parametrization of the SVI model is given by:

$w(x)=a+b(\rho *(x-m)+\sqrt{(x-m)^2 + \sigma ^2})$

where $w(x)$ is the total variance for determined time to maturity and $x=\log{K/S}$ is the moneyness with $K$ is the strike price and $S$ is the spot price. For a very good (and technical) discussion on the SVI model check this Gatheral´s paper. 

For this very first post on IV calibration, I´ll concentrate on single maturity curves, that is, a smile. This name appears because the IV curve as a function of the strike price looks like a person´s smile. One of the conditions of the calibration of a IV smile is the absence of butterfly arbitrage (see this post for a quant job question interview involving the derivation of this condition). More on this condition will be discussed in the session "Modeling the objective function" below.

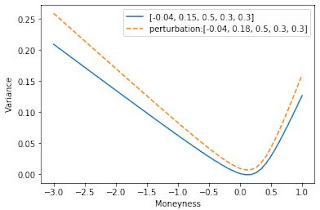
Before going further on the calibration of the SVI curve, it is important to take a look in the  role of each parameter in order to get a feeling of the bounds (also discussed below) in the optimization engine.

Parameter $a$ shifts the curve up and down.

Parameter $b$ changes the "angle" of the entire curve.

Parameter $m$ shifts the curve laterally.

Parameter $\rho$ modifies the curve in the low-moneyness region.

Parameter $\sigma$ changes the region close to null moneyness (at-the-money).

Modeling the objective function

The objective function OF is the function representing the fitting between the model and the empirical value to which the model is put against. In most of the cases, the OF is built in a manner that a perfect fitting leads to a null value of the OF. This is done by including the difference between the value from the model and the empirical model. The optimization engine tries to minimize the OF towards zero. In practice, a maximum tolerance is specified and the process stops when the value of the OF is within this tolerance.

In addition to the difference between model and empirical values, one might also consider penalizations for some situations which cannot be accepted by the nature of the problem being evaluated. In the case considered here, the adjusted curve of implied volatility cannot contain arbitrage opportunities. In addition, one should consider that the adjusted volatility should be within the bid-ask spread provided by the market data. For this post, I´m considering the following objective function:

$OF=min \sum_{K} [(\frac{\sigma_{model}}{\sigma_K}-1)^2 * e^{\eta_{butterfly}}*e^{\eta_{envelope}}]$

where $\eta_{butterfly}$ is one when the value of $g(x)$ is negative for determined strike price K and zero otherwise.  $\eta_{envelope}$ is zero if the adjusted value is within the bid-ask spread and $\eta_{butterfly}=(\sigma-\sigma_{average})/(spread)$ otherwise.
The implementation of the Black-Scholes formula is given here. The function $g(x)$ for the SVI model is given by:

$g(x)=[1-\frac{xw'}{2w}]^2 - \frac{w'^2}{4}(\frac{1}{w}+0.25)+\frac{w''}{2}$

where:

$w'(x)=b[\rho + \frac{(x-m)}{\sqrt{(x-m)^2 + \sigma^2}}]$

and

$w''(x)=\frac{b \sigma^2}{[(x-m)^2 + \sigma^2]^\frac{3}{2}}$

as mentioned before, the moneyness is $x=\log{K/S}$.

The envelope condition for the implied volatility requires the determination of a bid-ask spread from the option price quoted in the market. At a first glance, one could think of a mapping of the spread of the option price into the implied volatility by means of the greek vega (first derivative of the option price with respect to the volatility). However, this is not adequate since vega is a linear approximation, valid uniquely for small perturbations. Therefore, I decided to use a second optimization engine to recover the implied volatility for each single point of the data market, which also allows me to obtain the corresponding spread.
It is important to notice that the last function in the code sample above intends uniquely to change the order of the variables according to the standard required by the method scipy.optimize.differential_evolution (documentation). This is necessary when the callable function for the optimization process cannot be modified for being used in other parts of your code. Here the case is just illustrative.

Finally getting results

The final part of our simple optimization engine to calibrate SVI model is the call of the differential evolution algorithm:

First we get data from the market. I am using data provided by the site Barchart. The method getData() described above use pandas package to read a txt file, transferring data into a dataframe. This method also adds a moneyness column as well as the implied volatility (and corresponding spread) individually recovered form the market data (method described above).
The first argument of the differential_evolution method is the callable function that contains the objective function. The arguments of this callable are stored in the object args. The search space of the algorithm is specified by the bounds for each parameter. The callback argument specifies a function for follow-up of the optimization progress. The polish argument set to true indicates that the final value of the stochastic differential evolution algorithm is fine tuned by a deterministic gradient method.

Fitting of implied volatility

The first result is obtained with a vanilla European put option whose underlying asset are stocks of Apple (AAPL) negotiated in NASDAQ on November 23rd 2018. The time to maturity is one month and the spot price is $173.44. It is assumed 5% as the risk-free interest rate.
Due to the high liquidity of the Apple options one can barely notice the spread indicated by the error bars in the implied volatility curve. The lowest level of the implied volatility occurs close to the zero moneyness, that is, the point at which the strike price equals the spot price.

Using the SVI curve adjusted to the market data of implied volatility, we can calculate the option price using the Black-Scholes and compare it with the market prices. The calibration obtained with the simple model described here reproduces the overall behavior of the implied volatility as well as the option price curve. However, since the spread is not easily noticeable in the figures, we can check the relative error:

$error=\frac{x-average}{ask-bid}$

 The dashed red lines in the error plot denote the spread. A point close to the middle line means that the adjusted value is exactly above the midpoint between the bid-ask price spread. In the error plot, one can easily notice two distinct regions. The region with positive moneyness, that is, ITM for put options, almost all points lies within the bid-ask spread. Conversely, the region with negative moneyness, that is, OTM for put options, practically all points lies above the upper line, which indicates that calculated prices are above the ask prices in the market. This can be explained by the fact that the absolute spread in the ITM region is at least one order of magnitude higher than the spread in the OTM region, leading to difficulties in the calibration process in the OTM region.

I have mentioned in some paragraphs above that the black-box implementation of the differential evolution within the scipy optimization package requires two main parameters, named recombination and mutation. These parameters are directly related to the transformation of the candidate solutions towards the convergence. The value of these parameters alters the convergence velocity of the problem. A fast convergence might lead to a poor exploration of the search space, resulting in a solution corresponding to a local minimum instead of the global one. A slow convergence might consume computational resources beyond the necessary to solve the problem. In this sense, I present the convergence curve obtained with the fitting process of the Apple options using the default values of the black-box implementation: recombination$=0.7$ and mutation$=(0.5,1)$. The convergence rate is adequate in principle. However, it is worth noticing that due to the stochastic nature of the algorithm I should run several times the calibration to get an overview of the convergence process. I´ll let this task to the reader or maybe to a future post.
In the case of options whose underlying are Apple stocks a vast number of options as a function of the strike price are available in the market. For this case, the model presented here has proven to be satisfactory although some challenges remain in the OTM region. What if we consider a company with low level of option negotiation? How well does the model fit the empirical data? Challenge accepted.

  The next results were obtained with vanilla European call options of the company Star Bulk Carriers  (SBLK) also negotiated in NASDAQ. The time to maturity is 48 days, considering a spot price of $9.57 on December 12th 2018. While Apple data had more than a hundred points, the quote table for the Star Bulk Carriers has only seven points!
 The results for the fitting of the implied volatility are presented on the right. In principle, it is not so intuitive to draw a pattern for the market data (blue dots) as it was in the former results for Apple. We can also noticed that the error bars also considerably larger than in the previous case. In addition, at least three points have implied volatility above one, what is quite high. As usual, close to the ATM region (zero moneyness) the error bars are small indicating higher liquidity in the this region whereas the large spread in the other regions indicates lower liquidity.
The black dashed line is the fitted curve obtained with the calibration model described in this post. The fitting is not so bad considering the simplicity of my assumptions and approaches here. The main problem with this fitting relies in the two points close to the ATM, which are the most significant in terms of the traded volume of options. We still need to evaluate the fitting of the options prices, shown in the figure on the left. The overall behavior of the option prices are reproduced by the adjusted curve, despite the point with moneyness $x=0.25$.


The error plot clearly shows two points  out of the bid-ask spread. This result combined with low liquidity of the options for the considered company indicates that the approach for penalization of adjusted values out of the bid-ask spread should be revised. I am assuming that SVI is an adequate model for the implied volatility (several authors discuss about how good are the SVI curves).
Finally, we can take a look at the convergence curves. As expected, the number of required iterations is at least the double of the necessary in the fitting of the previous case. This is coherent with the fact that although less points are available, the distribution pattern of these points is not clearly a smile curve.

 

Regarding the convergence rate, one can notice that after around fifty iterations the objective function got stuck in a stable plateau with slight changes in the value of the objective function. This might indicate that for more challenging calibrations one should consider a better evaluation of the recombination and mutation parameters (actually I´m lying, this is not entirely true since we are not getting any statistics that grounds this conclusion. But I´ll let this task for the reader or maybe to another post).

I really hope you enjoyed the post that was carefully prepared for you! Leave your comments and suggestions!

May the Force be with you!

#=================================
Diogo de Moura Pedroso
LinkedIn: www.linkedin.com/in/diogomourapedroso